How To Find Intercepts Of A Rational Function

Finding Intercepts of Rational Fractions

Intercepts are the points at which a graph crosses either the x or y centrality, and they are very useful in sketching functions.

To find the y-intercept(s) (the betoken where the graph crosses the y-axis), substitute in 0 for x and solve for y or f(ten).

To find the x-intercept(s) (the point where the graph crosses the x-axis â€" also known equally zeros), substitute in 0 for y and solve for x.

Examples: Observe the intercepts of the part given.

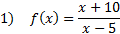
To find the y-intercept, nosotros must substitute in 0 for each x:

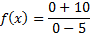
And then simplify:

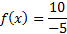
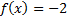
At that place is a y-intercept at 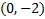. (Discover that 0 is the ten coordinate because on the y-axis, 10 = 0.)

To detect the x-intercept, nosotros must substitute in 0 for y or f(x):

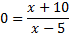
And then solve by cross-multiplying:

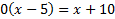
0 = x + 10

10 = -10

In that location is a y-intercept at 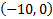. (Notice that 0 is the y coordinate considering on the x-axis, y = 0.)

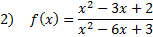
To observe the y-intercept, nosotros must substitute in 0 for each x:

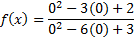
And and then simplify:

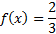
There is a y-intercept at .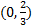

To find the x-intercept, we must substitute in 0 for y or f(ten):

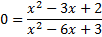
And and then solve by cross-multiplying:

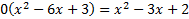
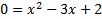
We must now solve the quadratic either past factoring or past using the quadratic formula.
We tin factor this trinomial, so we'll utilise that method:

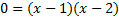
In that location are y-intercepts at .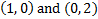

Notation: Not all rational functions have both an x or y intercept. If y'all cannot find a existent solution, then it does not have that intercept.

Practise: Detect the x and y intercepts of each rational function:

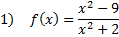
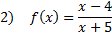
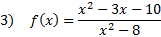
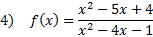
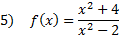
Answers: 1)ten-int. 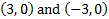y-int. 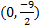2) x-int. (4, 0) y-int. 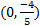iii) x-int. (-2, 0) and (5, 0) y-int 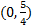4) ten-int. (1, 0) and (4, 0) y-int (0, -four) 5) x-int: none y-int: (0, -2)