How To Find The Real Zeros Of A Polynomial

3.three: Real Zeros of Polynomials

Last updated
Save equally PDF

Page ID: 3992

$Stitz.png$
Professor Emeritus (Chemistry) at Lakeland Customs Higher & Lorain County Customs Higher

In Section 3.2, we found that we can apply constructed division to decide if a given real number is a zero of a polynomial function. This section presents results which volition help us determine expert candidates to test using constructed partitioning. There are two approaches to the topic of finding the real zeros of a polynomial. The starting time approach (which is gaining popularity) is to utilize a little scrap of Mathematics followed by a practiced utilize of technology like graphing calculators. The second approach (for purists) makes good use of mathematical machinery (theorems) just. For completeness, we include the ii approaches merely in dissever subsections. Both approaches benefit from the following two theorems, the first of which is due to the famous mathematician Augustin Cauchy. Information technology gives united states of america an interval on which all of the real zeros of a polynomial can be found.

Theorem 3.8: Cauchy'southward Bound

Suppose

\[f(x) = a_{north} x^{n} + a_{due north-ane }ten^{n-1 } + \ldots + a_{i } ten + a_{0 }\]

is a polynomial of degree $north$ with $n \geq 1$. Permit $M$ be the largest of the numbers:

\[\dfrac{|a_{0}|}{|a_{due north}|}, \dfrac{|a_{1}|}{|a_{n}|}, \ldots, \dfrac{|a_{n-1}|}{|a_{northward}|}\]

And so all the real zeros of $f$ lie in in the interval $[-(M+ane),K+1]$.

The proof of this fact is non hands explained within the confines of this text. Like many of the results in this section, Cauchy'south Leap is all-time understood with an case.

Example $\PageIndex{one}$:

Allow $f(x) = 2x^4+4x^three-x^2-6x-3$. Decide an interval which contains all of the real zeros of $f$.

Solution

To find the $M$ stated in Cauchy'due south Bound, we take the accented value of leading coefficient, in this case $|2| = 2$ and split it into the largest (in absolute value) of the remaining coefficients, in this case $|-half-dozen| = 6$. We find $M=3$, so it is guaranteed that the real zeros of $f$ all lie in $[-four,4]$.

Whereas the previous result tells u.s.a. where we tin discover the real zeros of a polynomial, the next theorem gives united states a listing of possible real zeros.

Theorem 3.nine: Rational Zeros Theorem

Suppose $f(x) = a_{n} ten^{n} + a_{n-1 }x^{due north-one } + \ldots + a_{1 } ten + a_{0 }$ is a polynomial of degree $northward$ with $n \geq 1$, and $a_{0 }$, $a_{1 }$, ... $a_{due north}$ are integers. If $r$ is a rational cypher of $f$, then $r$ is of the form $\pm \frac{p}{q}$, where $p$ is a factor of the constant term $a_{0 }$, and $q$ is a factor of the leading coefficient $a_{n}$.

The Rational Zeros Theorem gives us a list of numbers to attempt in our constructed division and that is a lot nicer than merely guessing. If none of the numbers in the listing are zeros, then either the polynomial has no real zeros at all, or all of the existent zeros are irrational numbers. To encounter why the Rational Zeros Theorem works, suppose $c$ is a goose egg of $f$ and $c = \frac{p}{q}$ in lowest terms. This means $p$ and $q$ take no mutual factors. Since $f(c) = 0$, nosotros have

\[a_{n} \left(\dfrac{p}{q}\right)^{n} + a_{n-i}\left(\frac{p}{q}\right)^{n-ane} + \ldots + a_{ane} \left(\frac{p}{q}\right) + a_{0} = 0.\]

Multiplying both sides of this equation past $q^n$, we clear the denominators to get

\[a_{northward}p^{northward} + a_{n-1}p^{due north-i}q + \ldots + a_{one}p q^{due north-1} + a_{0}q^due north = 0\]

Rearranging this equation, we get

\[a_{n}p^{north} = -a_{n-ane}p^{n-1}q - \ldots - a_{ane}p q^{n-1} -a_{0}q^n\]

Now, the left hand side is an integer multiple of $p$, and the right hand side is an integer multiple of $q$. (Can you see why?) This means $a_{northward}p^{north}$ is both a multiple of $p$ and a multiple of $q$. Since $p$ and $q$ have no common factors, $a_{n}$ must be a multiple of $q$. If we rearrange the equation

\[a_{north}p^{n} + a_{n-1}p^{northward-one }q + \ldots + a_{1 }p q^{n-one } + a_{ 0 }q^n = 0\]

equally

\[a_{ 0 }q^due north = -a_{n}p^{northward} - a_{n- ane }p^{n- 1 }q - \ldots - a_{ ane }p q^{due north- 1 }\]

nosotros can play the same game and conclude $a_{ 0 }$ is a multiple of $p$, and nosotros have the result.

Example $\PageIndex{two}$:

Let $f(x) = 2x^four+4x^3-x^2-6x-3$. Use the Rational Zeros Theorem to list all of the possible rational zeros of $f$.

Solution

To generate a complete list of rational zeros, we need to have each of the factors of constant term, $a_{ 0 } = -three$, and divide them by each of the factors of the leading coefficient $a_{ 4 } = 2$. The factors of $-iii$ are $\pm \, 1$ and $\pm \, 3$. Since the Rational Zeros Theorem tacks on a $\pm$ anyway, for the moment, we consider only the positive factors $1$ and $3$. The factors of $2$ are $1$ and $2$, so the Rational Zeros Theorem gives the list $\left\{\pm \, \frac{1}{1}, \pm \, \frac{1}{2}, \pm \, \frac{3}{ane}, \pm \, \frac{3}{ii}\right\}$ or $\left\{\pm \, \frac{i}{2}, \pm \, 1, \pm \, \frac{3}{2}, \pm \, 3\right\}$.

Our give-and-take now diverges between those who wish to employ technology and those who practise not.

For Those Wishing to employ a Graphing Calculator

At this phase, we know not just the interval in which all of the zeros of $f(x) = 2x^4+4x^3-x^2-6x-iii$ are located, just we likewise know some potential candidates. We can now utilise our calculator to help us determine all of the existent zeros of $f$, as illustrated in the adjacent example.

Case $\PageIndex{three}$:

Let $f(x) = 2x^iv+4x^three-x^ii-6x-3$.

Graph $y=f(10)$ on the calculator using the interval obtained in Example 3.3.one as a guide.
Use the graph to shorten the listing of possible rational zeros obtained in Example 3.3.2.
Use synthetic division to detect the real zeros of $f$, and country their multiplicities.

Solution

In Case 3.three.1, nosotros determined all of the real zeros of $f$ prevarication in the interval $[-four, 4]$. Nosotros set our window accordingly and get

$alt$

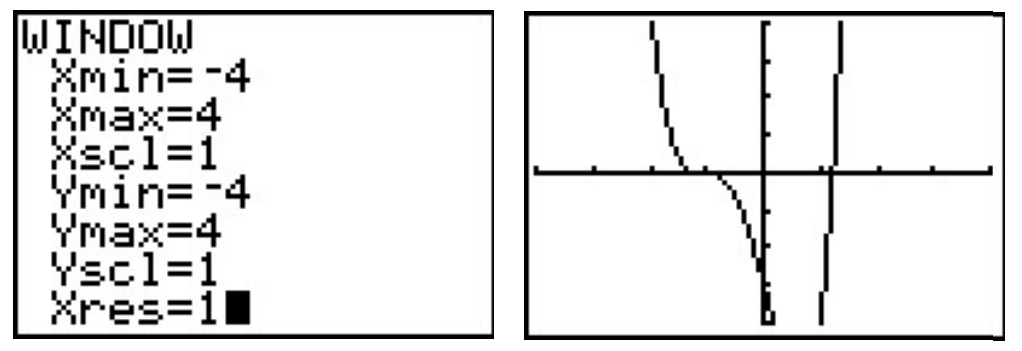
In Case 3.iii.ii, we learned that any rational zero of $f$ must be in the list $\left\{\pm \, \frac{one}{2}, \pm \, i, \pm \, \frac{3}{2}, \pm \, iii\right\}$. From the graph, it looks equally if we can rule out whatever of the positive rational zeros, since the graph seems to cross the $x$-axis at a value simply a little greater than $i$. On the negative side, $-1$ looks skilful, so we effort that for our synthetic division.

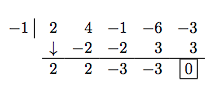
$3.3.3b.png$

We take a winner! Remembering that $f$ was a fourth caste polynomial, we know that our quotient is a third caste polynomial. If we can do one more successful sectionalisation, nosotros volition have knocked the caliber down to a quadratic, and, if all else fails, nosotros can use the quadratic formula to discover the concluding two zeros. Since there seems to be no other rational zeros to endeavor, nosotros go along with $-1$. Also, the shape of the crossing at $x = -one$ leads united states of america to wonder if the zero $ten = -one$ has multiplicity 3.

$3.3.3c.png$

Success! Our quotient polynomial is at present $2x^two - three$. Setting this to zero gives $2x^2 - 3 = 0$, or $10^2 = \frac{3}{2}$, which gives us $ten = \pm \, \frac{\sqrt{half-dozen}}{ii}$. Apropos multiplicities, based on our sectionalization, we have that $-ane$ has a multiplicity of at least $two$. The Factor Theorem tells united states our remaining zeros, $\pm \, \frac{\sqrt{6}}{2}$, each take multiplicity at least $1$. However, Theorem 3.vii tells us $f$ can take at most $4$ real zeros, counting multiplicity, and so nosotros conclude that $-1$ is of multiplicity exactly $2$ and $\pm \, \frac{\sqrt{6}}{2}$ each has multiplicity $1$. (Thus, we were \underline{wrong} to think that $-1$ had multiplicity $3$.)

It is interesting to note that we could greatly improve on the graph of $y=f(x)$ in the previous example given to us past the computer. For instance, from our conclusion of the zeros of $f$ and their multiplicities, we know the graph crosses at $x=-\frac{\sqrt{half dozen}}{2} \approx -1.22$ then turns back upwards to bear upon the $x-$centrality at \(x=-1$. This tells us that, despite what the estimator showed us the first fourth dimension, there is a relative maximum occurring at $x = -1$ and non a 'flattened crossing' equally we originally believed. After resizing the window, nosotros see non only the relative maximum but also a relative minimum just to the left of $x = -one$ which shows united states, once once more, that Mathematics enhances the engineering, instead of vice-versa. This is an case of what is called 'subconscious behavior'.

$alt$

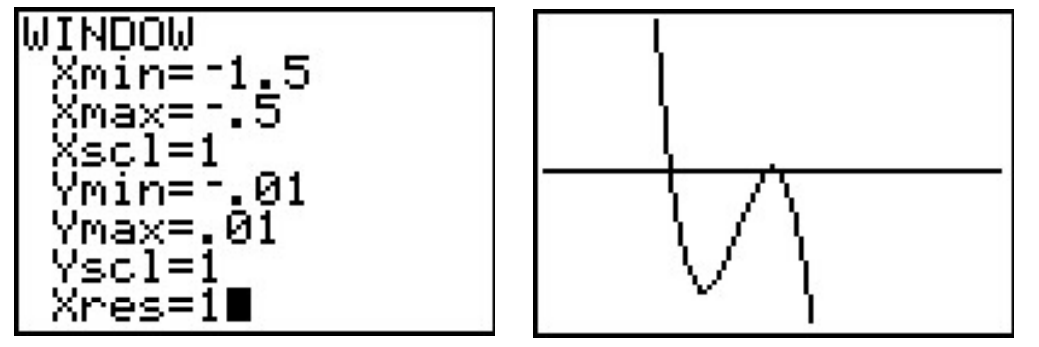
Our next example shows how even a mild-mannered polynomial can cause problems.

Instance $\PageIndex{4}$:

Let $f(10) = x^4 + ten^2 - 12$.

Use Cauchy's Leap to make up one's mind an interval in which all of the real zeros of $f$ prevarication.
Apply the Rational Zeros Theorem to determine a listing of possible rational zeros of $f$.
Graph $y=f(ten)$ using your graphing figurer.
Find all of the existent zeros of $f$ and their multiplicities.

Solution

1. Applying Cauchy's Bound, we observe $Chiliad = 12$, and then all of the real zeros lie in the interval $[-xiii,13]$.

2. Applying the Rational Zeros Theorem with constant term $a_{ 0 } = -12$ and leading coefficient $a_{ four } = ane$, we get the list $\{\pm \, i$, $\pm \, two$, $\pm \, three$, $\pm \, four$, $\pm \, six$, $\pm \, 12\}$.

3. Graphing $y=f(x)$ on the interval $[-13,13]$ produces the graph below on the left. Zooming in a bit gives the graph below on the right. Based on the graph, none of our rational zeros volition piece of work. (Exercise yous see why not?)

$alt$

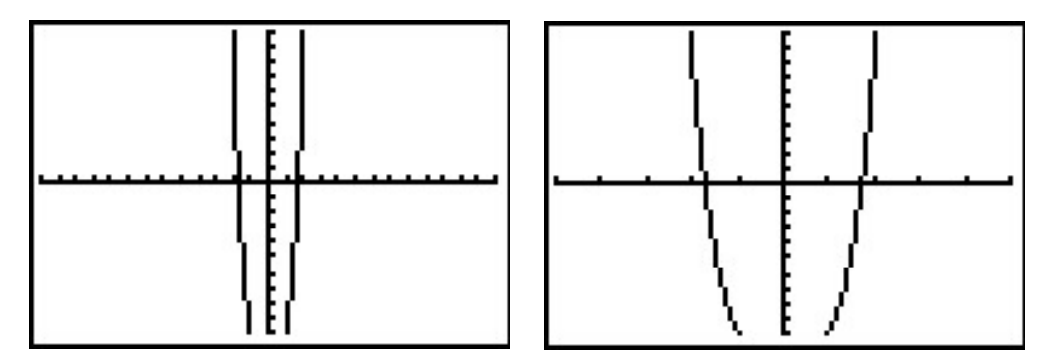
4. From the graph, we know $f$ has 2 real zeros, one positive, and one negative. Our just promise at this point is to try and find the zeros of $f$ by setting $f(10)=x^4+x^ii-12=0$ and solving. If we stare at this equation long enough, we may recognize it as a 'quadratic in disguise' or 'quadratic in form'. In other words, we have three terms: $x^iv$, $x^2$ and $12$, and the exponent on the offset term, $x^4$, is exactly twice that of the second term, $x^two$. We may rewrite this equally $\left(x^2\right)^two + \left(ten^2\right) - 12 = 0$. To better come across the woods for the trees, nosotros momentarily replace $x^2$ with the variable $u$. In terms of $u$, our equation becomes $u^ii + u - 12 = 0$, which we can readily factor as $(u+iv)(u-3) = 0$. In terms of $x$, this ways $10^iv+ten^2-12= \left(10^2-3\right) \left(10^2 + 4 \right)=0$. We get $x^2 = iii$, which gives us $x = \pm \sqrt{3}$, or $x^2=-4$, which admits no real solutions. Since $\sqrt{three} \approx i.73$, the ii zeros lucifer what we expected from the graph. In terms of multiplicity, the Cistron Theorem guarantees $\left(ten - \sqrt{3}\right)$ and $\left(x + \sqrt{3}\correct)$ are factors of $f(10)$. Since $f(ten)$ can be factored as $f(x) = \left(10^ii-3\right) \left(x^2 + 4 \correct)$, and $x^two + 4$ has no existent zeros, the quantities $\left(ten - \sqrt{iii}\correct)$ and $\left(10 + \sqrt{three}\correct)$ must both be factors of $x^2-3$. According to Theorem three.seven, $x^two-3$ can have at most $2$ zeros, counting multiplicity, hence each of $\pm \sqrt{3}$ is a cipher of $f$ of multiplicity $one$.

The technique used to cistron $f(x)$ in Instance 3.iii.4 is called $u$ -substitution. We shall see more than of this technique in Section 5.three. In general, substitution can help us place a 'quadratic in disguise' provided that at that place are exactly three terms and the exponent of the outset term is exactly twice that of the second. Information technology is entirely possible that a polynomial has no real roots at all, or worse, it has existent roots but none of the techniques discussed in this department can help united states find them exactly. In the latter example, we are forced to judge, which in this subsection ways nosotros use the 'Zero' command on the graphing figurer.

For Those Wishing NOT to use a Graphing Computer

Suppose we wish to find the zeros of $f(x) = 2x^4+4x^3-ten^2-6x-3$ without using the calculator. In this subsection, nosotros present some more than advanced mathematical tools (theorems) to help us. Our showtime event is due to Rene Descartes.

Theorem 3.ten: Descartes' Dominion of Signs

Suppose $f(x)$ is the formula for a polynomial function written with descending powers of $10$.

If $P$ denotes the number of variations of sign in the formula for $f(x)$, then the number of positive existent zeros (counting multiplicity) is one of the numbers $P, P-two, P-4, \ldots $.
If $N$ denotes the number of variations of sign in the formula for $f(-10)$, then the number of negative real zeros (counting multiplicity) is one of the numbers \{N\), $N-two$, $North-4$, \dots\}.

A few remarks are in club. Get-go, to use Descartes' Rule of Signs, nosotros need to sympathise what is meant by a variation in sign of a polynomial function. Consider $f(ten) = 2x^iv+4x^3-x^2-6x-three$. If we focus on just the signs of the coefficients, nosotros outset with a $(+)$, followed past another $(+)$, so switch to $(-)$, and stay $(-)$ for the remaining 2 coefficients. Since the signs of the coefficients switched once every bit we read from left to right, we say that $f(ten)$ has one variation in sign. When we speak of the variations in sign of a polynomial function $f$ we assume the formula for $f(x)$ is written with descending powers of $x$, as in Definition 3.1, and concern ourselves merely with the nonzero coefficients. Second, different the Rational Zeros Theorem, Descartes' Rule of Signs gives us an judge to the number of positive and negative real zeros, not the actual value of the zeros. Lastly, Descartes' Dominion of Signs counts multiplicities. This means that, for instance, if i of the zeros has multiplicity $ii$, Descsartes' Dominion of Signs would count this equally two zeros. Lastly, note that the number of positive or negative real zeros always starts with the number of sign changes and decreases by an even number. For instance, if $f(10)$ has $7$ sign changes, then, counting multplicities, $f$ has either $7$, $v$, $iii$ or $one$ positive real nix. This implies that the graph of $y=f(10)$ crosses the positive $10$-centrality at least once. If $f(-x)$ results in $iv$ sign changes, then, counting multiplicities, $f$ has $4$, $2$ or $0$ negative real zeros; hence, the graph of $y=f(10)$ may not cantankerous the negative $ten$-axis at all.

Example $\PageIndex{5}$:

Permit $f(x) = 2x^4+4x^3-ten^2-6x-three$. Use Descartes' Rule of Signs to make up one's mind the possible number and location of the real zeros of $f$.

Solution

As noted above, the variations of sign of $f(x)$ is $one$. This ways, counting multiplicities, $f$ has exactly $i$ positive real aught. Since

\[f(-x)=two(-ten)^iv+4(-x)^three-(-x)^two-six(-x)-3=2x^4-4x^3-10^2+6x-3\]

has $3$ variations in sign, $f$ has either $3$ negative existent zeros or $1$ negative real zilch, counting multiplicities.

Cauchy's Bound gives the states a full general leap on the zeros of a polynomial function. Our next result helps us determine bounds on the real zeros of a polynomial as we synthetically divide which are often sharper\footnote{That is, better, or more accurate.} bounds than Cauchy's Bound.

Theorem 3.one.one: Upper and Lower Bounds

Suppose $f$ is a polynomial of degree $northward \geq ane$.

If $c > 0$ is synthetically divided into $f$ and all of the numbers in the last line of the division tableau accept the same signs, so $c$ is an upper jump for the existent zeros of $f$. That is, in that location are no real zeros greater than $c$.
If $c < 0$ is synthetically divided into $f$ and the numbers in the final line of the division tableau alternate signs, and then $c$ is a lower spring for the existent zeros of $f$. That is, there are no real zeros less than $c$.

If the number $0$ occurs in the final line of the division tableau in either of the higher up cases, information technology tin be treated as $(+)$ or $(-)$ as needed.

The Upper and Lower Bounds Theorem works because of Theorem 3.4. For the upper bound part of the theorem, suppose $c>0$ is divided into $f$ and the resulting line in the division tableau contains, for example, all nonnegative numbers. This means $f(ten) = (10-c) q(x) + r$, where the coefficients of the quotient polynomial and the remainder are nonnegative. (Note that the leading coefficient of $q$ is the same as $f$ so $q(10)$ is non the zip polynomial.) If $b > c$, then $f(b) = (b-c) q(b) + r$, where $(b-c)$ and $q(b)$ are both positive and $r \geq 0$. Hence $f(b) > 0$ which shows $b$ cannot exist a zero of $f$. Thus no existent number $b > c$ can be a zero of $f$, equally required. A similar argument proves $f(b) < 0$ if all of the numbers in the final line of the synthetic division tableau are not-positive. To testify the lower bound part of the theorem, we note that a lower jump for the negative real zeros of $f(x)$ is an upper jump for the positive real zeros of $f(-ten)$. Applying the upper bound portion to $f(-x)$ gives the consequence. (Practise you see where the alternating signs come up in?) With the additional mathematical mechanism of Descartes' Rule of Signs and the Upper and Lower Bounds Theorem, nosotros tin can find the real zeros of $f(x) = 2x^4+4x^3-x^2-6x-3$ without the utilize of a graphing estimator.

Example $\PageIndex{6}$:

Let $f(10) = 2x^4+4x^iii-10^two-6x-3$.

Find all of the real zeros of $f$ and their multiplicities.
Sketch the graph of $y=f(x)$.

Solution

one. Nosotros know from Cauchy'south Leap that all of the existent zeros lie in the interval $[-4,iv]$ and that our possible rational zeros are $\pm \, \frac{ane}{2}$, $\pm \, one$, $\pm \, \frac{three}{ii}$ and $\pm \, 3$. Descartes' Rule of Signs guarantees the states at least i negative real zero and exactly ane positive real cipher, counting multiplicity. We effort our positive rational zeros, starting with the smallest, $\frac{1}{2}$. Since the remainder isn't zero, we know $\frac{i}{two}$ isn't a zero. Sadly, the final line in the division tableau has both positive and negative numbers, so $\frac{1}{2}$ is not an upper bound. The only information nosotros get from this division is courtesy of the Remainder Theorem which tells us $f\left(\frac{1}{2}\right) = -\frac{45}{8}$ and then the signal $\left(\frac{1}{2}, -\frac{45}{viii}\right)$ is on the graph of $f$. We continue to our adjacent possible goose egg, $one$. Equally before, the only information nosotros can glean from this is that $(one,-4)$ is on the graph of $f$. When nosotros attempt our next possible zilch, $\frac{3}{ii}$, we get that information technology is non a cypher, and we also see that it is an upper bound on the zeros of $f$, since all of the numbers in the final line of the partition tableau are positive. This means in that location is no point trying our last possible rational zero, $3$. Descartes' Dominion of Signs guaranteed us a positive real zero, and at this bespeak nosotros accept shown this null is irrational. Furthermore, the Intermediate Value Theorem, Theorem 3.i, tells us the zero lies between $i$ and $\frac{iii}{2}$, since $f(one) < 0$ and $f\left(\frac{three}{2}\right) > 0$.

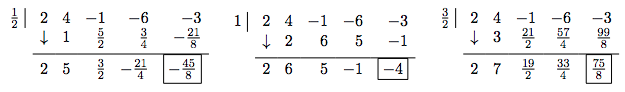
$3.3.6a.png$

2. We now turn our attending to negative real zeros. We try the largest possible zippo, $-\frac{1}{2}$. Synthetic division shows united states it is non a zero, nor is it a lower bound (since the numbers in the final line of the segmentation tableau exercise not alternate), so we proceed to $-1$. This division shows $-one$ is a zero. Descartes' Rule of Signs told us that we may have up to three negative real zeros, counting multiplicity, so we try $-1$ once more, and it works once again. At this point, we have taken $f$, a fourth degree polynomial, and performed two successful divisions. Our quotient polynomial is quadratic, then we look at information technology to find the remaining zeros.

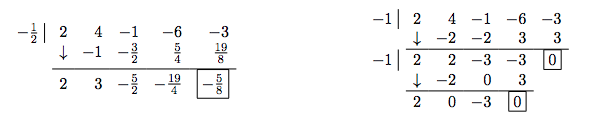
$3.3.6b.png$

Setting the quotient polynomial equal to nothing yields $2x^2 - 3 = 0$, and then that $x^2 = \frac{3}{two}$, or $x = \pm \, \frac{\sqrt{6}}{ii}$. Descartes' Rule of Signs tells us that the positive real zero we found, $\frac{\sqrt{6}}{2}$, has multiplicity $1$. Descartes too tells us the total multiplicity of negative real zeros is $3$, which forces $-1$ to be a zero of multiplicity $two$ and $- \frac{\sqrt{half dozen}}{2}$ to have multiplicity $1$.

Nosotros know the end behavior of $y=f(x)$ resembles that of its leading term $y=2x^four$. This ways that the graph enters the scene in Quadrant II and exits in Quadrant I. Since $\pm \, \frac{\sqrt{6}}{2}$ are zeros of odd multiplicity, we have that the graph crosses through the $ten$-axis at the points $\left( -\frac{\sqrt{vi}}{ii}, 0 \correct)$ and $\left( \frac{\sqrt{6}}{2}, 0 \correct)$. Since $-ane$ is a nothing of multiplicity $2$, the graph of $y=f(ten)$ touches and rebounds off the $x$-centrality at $(-ane,0)$. Putting this together, we get

$alt$

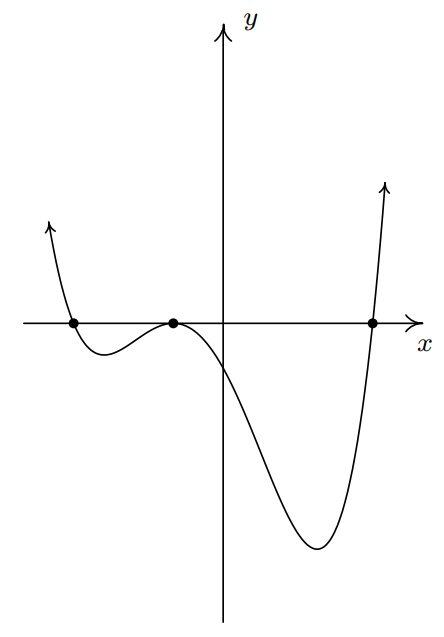
You can meet why the 'no computer' approach is not very popular these days. Information technology requires more computation and more theorems than the alternative (this is apparently a bad thing). In general, no matter how many theorems y'all throw at a polynomial, it may well be impossible to find their zeros exactly (it can exist proven that the zeros of some polynomials cannot be expressed using the usual algebraic symbols). The polynomial $f(ten) = x^5-ten-i$ is one such animate being.

According to Descartes' Rule of Signs, $f$ has exactly 1 positive existent nada, and it could take ii negative existent zeros, or none at all. The Rational Zeros Test gives us $\pm one$ as rational zeros to try but neither of these work since $f(1) = f(-1) = -one$. If we attempt the substitution technique nosotros used in Example 3.3.4, we observe $f(10)$ has iii terms, simply the exponent on the $10^five$ isn't exactly twice the exponent on $ten$. How could we go virtually approximating the positive zero without resorting to the 'Zero' command of a graphing computer? We use the Bisection Method. The first step in the Bisection Method is to find an interval on which $f$ changes sign. We know $f(ane) = -1$ and we detect $f(2) = 29$. Past the Intermediate Value Theorem, we know that the zero of $f$ lies in the interval $[1,2]$. Next, nosotros 'bifurcate' this interval and discover the midpoint is $1.5$. We have that $f(i.5)\approx 5.09$. This means that our zero is between $ane$ and $1.five$, since $f$ changes sign on this interval. Now, nosotros 'bisect' the interval $[1,1.5]$ and find $f(ane.25) \approx 0.80$, then now we have the zero betwixt $one$ and $1.25$. Bisecting $[1,1.25]$, we find $f(i.125) \approx -0.32$, which means the zero of $f$ is between $1.125$ and $one.25$. We continue in this fashion until we have 'sandwiched' the cypher betwixt two numbers which differ past no more a desired accuracy. You can think of the Bisection Method as reversing the sign diagram procedure: instead of finding the zeros and checking the sign of $f$ using examination values, we are using test values to decide where the signs switch to observe the zeros. It is a slow and tiresome, yet fool-proof, method for approximating a real zero.

Our next example reminds u.s.a. of the office finding zeros plays in solving equations and inequalities.

Example $\PageIndex{seven}$:

Find all of the existent solutions to the equation $2x^5+6x^3+3 = 3x^4+8x^2$.
Solve the inequality $2x^5+6x^3+3 \leq 3x^4+8x^2$.
Interpret your answer to part 2 graphically, and verify using a graphing figurer.

Solution

1. Finding the real solutions to $2x^5+6x^three+iii = 3x^4+8x^2$ is the same as finding the real solutions to $2x^five-3x^4+6x^iii-8x^2+3=0$. In other words, we are looking for the real zeros of $p(ten)= 2x^5-3x^4+6x^three-8x^2+three$. Using the techniques developed in this section, we get

$alt$

The caliber polynomial is $2x^2 + half dozen$ which has no real zeros and so we get $x=-\frac{1}{2}$ and $x=1$.

2. To solve this nonlinear inequality, we follow the same guidelines ready forth in Section 2.4: we get $0$ on one side of the inequality and construct a sign diagram. Our original inequality can be rewritten equally $2x^5-3x^4+6x^3-8x^2+iii \leq 0$. We found the zeros of $p(x) = 2x^5-3x^4+6x^3-8x^two+3$ in part ane to be $x=-\frac{1}{two}$ and $ten=1$. We construct our sign diagram equally before.

$alt$

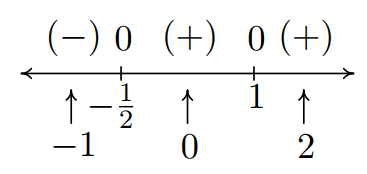
The solution to $p(10) < 0$ is $\left(-\infty, -\frac{1}{two}\right)$, and we know $p(x) = 0$ at $x=-\frac{i}{2}$ and $x=1$. Hence, the solution to $p(x) \leq 0$ is $\left(-\infty, -\frac{1}{2}\right] \cup \left\{1\correct\}$.

3. To interpret this solution graphically, we prepare $f(x) = 2x^five+6x^3+3$ and $thousand(x) = 3x^four+8x^2$. We retrieve that the solution to $f(x) \leq chiliad(x)$ is the fix of $ten$ values for which the graph of $f$ is below the graph of $g$ (where $f(x) < g(x)$ along with the $ten$ values where the two graphs intersect $f(x) = 1000(10)$. Graphing $f$ and $g$ on the calculator produces the picture on the lower left. (The end behavior should tell you which is which.) We see that the graph of $f$ is below the graph of $1000$ on $\left(-\infty, -\frac{1}{2}\right)$. Yet, it is difficult to see what is happening nigh $x=ane$. Zooming in (and making the graph of $one thousand$ thicker), we come across that the graphs of $f$ and $g$ do intersect at $x=1$, but the graph of $g$ remains beneath the graph of $f$ on either side of $x = 1$.

$alt$

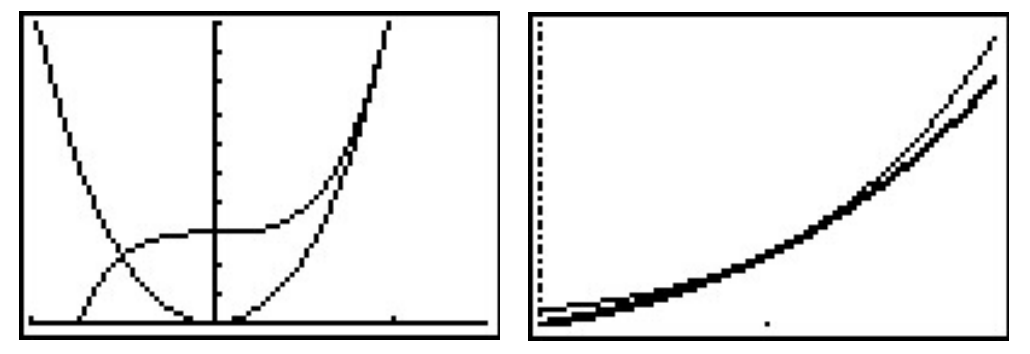
Our last example revisits an application in the Exercises of Section 3.1.

Example $\PageIndex{8}$:

Suppose the profit $P$, in thousands of dollars, from producing and selling $x$ hundred LCD TVs is given past $P(x)=-5x^iii+35x^2-45x-25$, $0 \leq x \leq x.07$. How many TVs should be produced to make a profit? Check your answer using a graphing utility.

Solution

To 'make a profit' means to solve $P(x) = -5x^iii+35x^2-45x-25 > 0$, which we do analytically using a sign diagram. To simplify things, we first factor out the $-5$ common to all the coefficients to get

\[-five\left(ten^3 - 7x^2+9x-five\right) > 0\]

so we can just focus on finding the zeros of $f(x) = x^three-7x^2+9x+v$. The possible rational zeros of $f$ are $\pm ane$ and $\pm 5$, and going through the usual computations, nosotros find $x=5$ is the only rational zero. Using this, we factor $f(ten) = x^3-7x^2+9x+5 = (x-v) \left(ten^2-2x-one\correct)$, and nosotros find the remaining zeros past applying the Quadratic Formula to $x^ii-2x-ane = 0$. We detect 3 real zeros, $x=1-\sqrt{two} = -0.414 \ldots$, $x = ane+\sqrt{2} = 2.414 \ldots$, and $x = 5$, of which only the concluding 2 fall in the applied domain of $[0, ten.07]$. We choose $x=0$, $x=3$ and $ten=10.07$ as our test values and plug them into the role $P(x)=-5x^3+35x^2-45x-25$ (non $f(x) =ten^3 - 7x^2+9x-five$) to get the sign diagram below.

$alt$

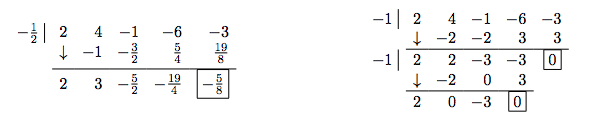
We see immediately that $P(x)>0$ on $(one+\sqrt{ii},five)$. Since $ten$ measures the number of TVs in hundreds, $x = 1 + \sqrt{2}$ corresponds to $241.4\ldots$ TVs. Since we can't produce a partial part of a Goggle box, nosotros demand to cull betwixt producing 241 and 242 TVs. From the sign diagram, we run into that $P(2.41) < 0$ but $P(2.42)>0$ and so, in this instance we take the adjacent larger integer value and set the minimum production to 242 TVs. At the other finish of the interval, we accept $10=5$ which corresponds to $500$ TVs. Here, we accept the next smaller integer value, $499$ TVs to ensure that we make a turn a profit. Hence, in social club to make a profit, at to the lowest degree 242, just no more than than 499 TVs demand to be produced. To check our answer using a reckoner, we graph $y=P(10)$ and make use of the 'Nil' command. We see that the calculator approximations deport out our analysis.

$alt$

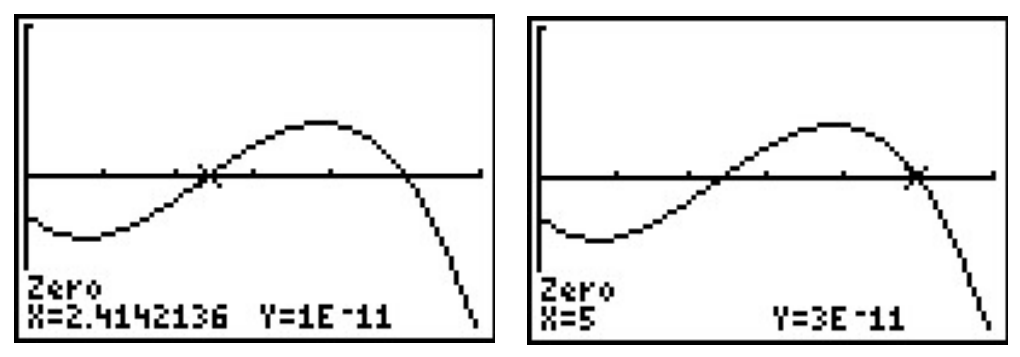
Note that the $y$-coordinates of the points here aren't registered as $0$. They are expressed in Scientific Annotation. For instance, $one E-xi$ corresponds to $0.00000000001$, which is pretty close in the calculator's optics to $0$ (but not a Mathematician'south).

Contributors and Attributions

Carl Stitz, Ph.D. (Lakeland Community College) and Jeff Zeager, Ph.D. (Lorain County Community College)

Source: https://math.libretexts.org/Bookshelves/Precalculus/Book%3A_Precalculus_(StitzZeager)/03%3A_Polynomial_Functions/3.03%3A_Real_Zeros_of_Polynomials

Posted by: gravescolmilluke.blogspot.com