how to find the derivative of a graph

3.2: The Derivative as a Role

1. Last updated

2. Save as PDF

Page ID

2491

Learning Objectives

• Define the derivative part of a given function.
• Graph a derivative function from the graph of a given function.
• Country the connection between derivatives and continuity.
• Describe three atmospheric condition for when a role does non have a derivative.
• Explicate the significant of a higher-order derivative.

As nosotros accept seen, the derivative of a function at a given point gives us the rate of change or slope of the tangent line to the function at that point. If we differentiate a position function at a given time, nosotros obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every indicate would produce valuable data about the behavior of the office. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would rapidly become quite tedious. In this section we define the derivative part and larn a procedure for finding it.

Derivative Functions

The derivative function gives the derivative of a role at each point in the domain of the original office for which the derivative is defined. Nosotros can formally define a derivative function every bit follows.

Definition: Derivative Role

Let \(f\) be a function. The derivative function, denoted by \(f'\), is the part whose domain consists of those values of \(x\) such that the following limit exists:

\[f'(x)=\lim_{h→0}\frac{f(x+h)−f(10)}{h}. \label{derdef}\]

A function \(f(x)\) is said to exist differentiable at \(a\) if \(f'(a)\) exists. More generally, a role is said to be differentiable on \(S\) if information technology is differentiable at every point in an open set \(S\), and a differentiable function is i in which \(f'(x)\) exists on its domain.

In the side by side few examples we use Equation \ref{derdef} to detect the derivative of a office.

Example \(\PageIndex{1}\): Finding the Derivative of a Foursquare-Root Function

Find the derivative of \(f(x)=\sqrt{x}\).

Solution

Showtime directly with the definition of the derivative function.

Substitute \(f(x+h)=\sqrt{x+h}\) and \(f(x)=\sqrt{ten}\) into \(f'(x)= \displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\).

\(f'(ten)=\displaystyle \lim_{h→0}\frac{\sqrt{x+h}−\sqrt{ten}}{h}\)
\(=\displaystyle\lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}⋅\frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{ten+h}+\sqrt{10}}\)	Multiply numerator and denominator by \(\sqrt{x+h}+\sqrt{ten}\) without distributing in the denominator.
\(=\displaystyle\lim_{h→0}\frac{h}{h\left(\sqrt{10+h}+\sqrt{ten}\right)}\)	Multiply the numerators and simplify.
\(=\displaystyle\lim_{h→0}\frac{1}{\left(\sqrt{x+h}+\sqrt{x}\correct)}\)	Cancel the \(h\).
\(=\dfrac{1}{2\sqrt{x}}\)	Evaluate the limit

Example \(\PageIndex{two}\): Finding the Derivative of a Quadratic Function

Find the derivative of the function \(f(x)=x^2−2x\).

Solution

Follow the same procedure here, but without having to multiply by the cohabit.

Substitute \(f(10+h)=(10+h)^two−2(x+h)\) and \(f(x)=ten^2−2x\) into \(f'(x)= \displaystyle \lim_{h→0}\frac{f(ten+h)−f(x)}{h}.\)

\(f'(x)=\displaystyle\lim_{h→0}\frac{((10+h)^2−2(x+h))−(ten^2−2x)}{h}\)
\(=\displaystyle\lim_{h→0}\frac{x^2+2xh+h^2−2x−2h−x^2+2x}{h}\)	Aggrandize \((10+h)^2−2(x+h)\).
\(=\displaystyle\lim_{h→0}\frac{2xh−2h+h^2}{h}\)	Simplify
\(=\displaystyle\lim_{h→0}\frac{h(2x−ii+h)}{h}\)	Cistron out \(h\) from the numerator
\(=\displaystyle\lim_{h→0}(2x−2+h)\)	Abolish the common factor of \(h\)
\(=2x−ii\)	Evaluate the limit

Practice \(\PageIndex{i}\)

Observe the derivative of \(f(x)=x^2\).

Hint

Employ Equation \ref{derdef} and follow the case.

Respond

\(f'(x)=2x\)

We utilise a diverseness of different notations to express the derivative of a function. In Example we showed that if \(f(x)=x^2−2x\), and so \(f'(x)=2x−2\). If nosotros had expressed this function in the course \(y=10^two−2x\), we could have expressed the derivative as \(y′=2x−2\) or \(\dfrac{dy}{dx}=2x−2\). We could have conveyed the same information by writing \(\dfrac{d}{dx}\left(x^2−2x\right)=2x−two\). Thus, for the role \(y=f(x)\), each of the following notations represents the derivative of \(f(10)\):

\(f'(ten), \quad \dfrac{dy}{dx}, \quad y′,\quad \dfrac{d}{dx}\big(f(x)\big)\).

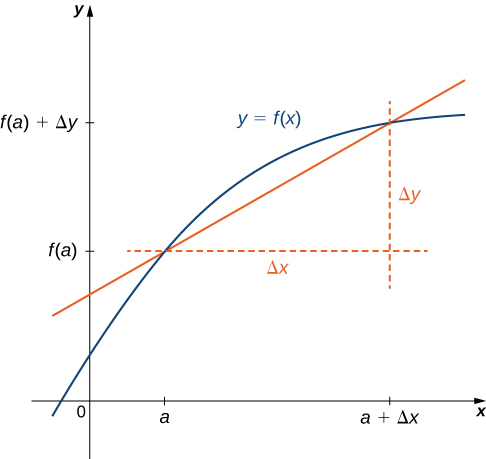
In place of \(f'(a)\) we may also utilise \(\dfrac{dy}{dx}\Big|_{x=a}\). Employ of the \(\dfrac{dy}{dx}\) note (called Leibniz annotation) is quite mutual in engineering and physics. To understand this notation amend, call up that the derivative of a function at a signal is the limit of the slopes of secant lines equally the secant lines approach the tangent line. The slopes of these secant lines are often expressed in the form \(\dfrac{Δy}{Δx}\) where \(Δy\) is the divergence in the \(y\) values respective to the difference in the \(x\) values, which are expressed as \(Δx\) (Effigy \(\PageIndex{1}\)). Thus the derivative, which can exist thought of equally the instantaneous charge per unit of change of \(y\) with respect to \(x\), is expressed equally

\(\displaystyle \frac{dy}{dx}= \lim_{Δx→0}\frac{Δy}{Δx}\).

Effigy \(\PageIndex{i}\): The derivative is expressed as \(\dfrac{dy}{dx}=\displaystyle\lim_{Δx→0}\frac{Δy}{Δx}\).

Graphing a Derivative

We accept already discussed how to graph a function, so given the equation of a function or the equation of a derivative function, we could graph information technology. Given both, we would expect to see a correspondence between the graphs of these two functions, since \(f'(x)\) gives the charge per unit of alter of a function \(f(x)\) (or slope of the tangent line to \(f(x)\)).

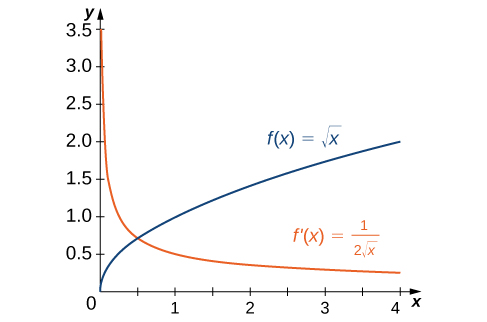
In Example \(\PageIndex{1}\), we found that for \(f(x)=\sqrt{x}\), \(f'(x)=\frac{ane}{two\sqrt{x}}\). If we graph these functions on the same axes, every bit in Figure \(\PageIndex{2}\), we can use the graphs to sympathize the relationship between these ii functions. First, we notice that \(f(x)\) is increasing over its entire domain, which ways that the slopes of its tangent lines at all points are positive. Consequently, we expect \(f'(x)>0\) for all values of ten in its domain. Furthermore, every bit \(x\) increases, the slopes of the tangent lines to \(f(10)\) are decreasing and nosotros expect to see a respective decrease in \(f'(10)\). We also discover that \(f(0)\) is undefined and that \(\displaystyle \lim_{x→0^+}f'(ten)=+∞\), corresponding to a vertical tangent to \(f(x)\) at \(0\).

Figure \(\PageIndex{ii}\): The derivative \(f'(x)\) is positive everywhere because the role \(f(x)\) is increasing.

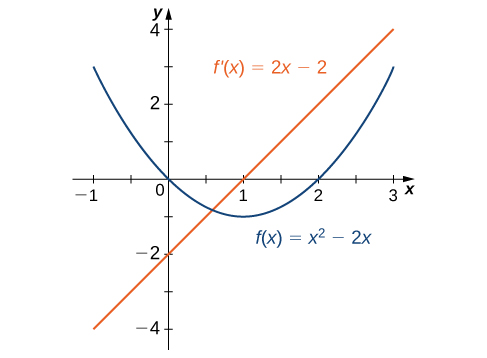
In Example \(\PageIndex{ii}\), we plant that for \(f(x)=x^ii−2x,\; f'(x)=2x−two\). The graphs of these functions are shown in Effigy \(\PageIndex{three}\). Observe that \(f(x)\) is decreasing for \(x<1\). For these same values of \(10\), \(f'(x)<0\). For values of \(10>i\), \(f(x)\) is increasing and \(f'(ten)>0\). Also, \(f(ten)\) has a horizontal tangent at \(x=1\) and \(f'(1)=0\).

Effigy \(\PageIndex{3}\): The derivative \(f'(x)<0\) where the function \(f(x)\) is decreasing and \(f'(ten)>0\) where \(f(x)\) is increasing. The derivative is zero where the part has a horizontal tangent

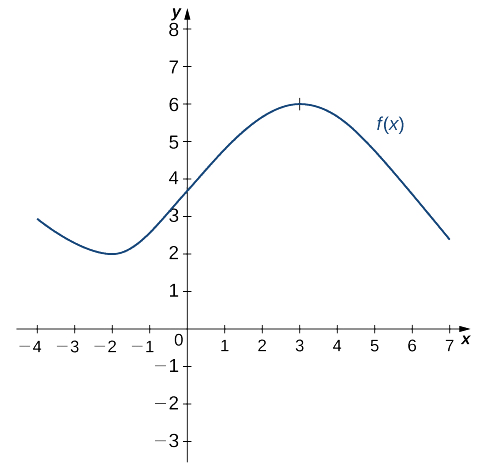
Instance \(\PageIndex{3}\): Sketching a Derivative Using a Part

Use the following graph of \(f(x)\) to sketch a graph of \(f'(x)\).

Solution

The solution is shown in the post-obit graph. Observe that \(f(x)\) is increasing and \(f'(x)>0\) on \((–2,3)\). Also, \(f(x)\) is decreasing and \(f'(10)<0\) on \((−∞,−2)\) and on \((3,+∞)\). Also note that \(f(x)\) has horizontal tangents at \(–two\) and \(3\), and \(f'(−2)=0\) and \(f'(3)=0\).

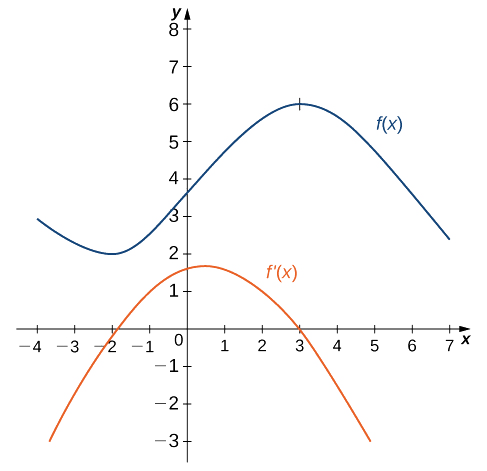
Practise \(\PageIndex{2}\)

Sketch the graph of \(f(10)=10^2−4\). On what interval is the graph of \(f'(x)\) above the \(10\)-axis?

Hint

The graph of \(f'(10)\) is positive where \(f(ten)\) is increasing.

Reply

\((0,+∞)\)

Derivatives and Continuity

Now that we tin can graph a derivative, allow'due south examine the behavior of the graphs. First, we consider the human relationship betwixt differentiability and continuity. Nosotros will encounter that if a function is differentiable at a point, it must be continuous there; however, a function that is continuous at a point need not be differentiable at that betoken. In fact, a function may be continuous at a signal and fail to be differentiable at the bespeak for i of several reasons.

Differentiability Implies Continuity

Permit \(f(x)\) be a office and \(a\) be in its domain. If \(f(x)\) is differentiable at \(a\), then \(f\) is continuous at \(a\).

Proof

If \(f(x)\) is differentiable at \(a\), so \(f'(a)\) exists and, if we let \(h = ten - a\), we accept \( x = a + h \), and every bit \(h=x-a\to 0\), we tin come across that \(x\to a\).

Then

\[ f'(a) = \lim_{h\to 0}\frac{f(a+h)-f(a)}{h}\nonumber\]

tin can be rewritten equally

\(f'(a)=\displaystyle \lim_{x→a}\frac{f(x)−f(a)}{x−a}\).

We want to show that \(f(ten)\) is continuous at \(a\) by showing that \(\displaystyle \lim_{x→a}f(ten)=f(a).\) Thus,

\(\brainstorm{marshal*} \displaystyle \lim_{x→a}f(x) &=\lim_{x→a}\;\large(f(x)−f(a)+f(a)\large)\\[4pt]
&=\lim_{x→a}\left(\frac{f(x)−f(a)}{10−a}⋅(10−a)+f(a)\correct) & & \text{Multiply and divide }(f(10)−f(a))\text{ by }x−a.\\[4pt]
&=\left(\lim_{x→a}\frac{f(ten)−f(a)}{x−a}\correct)⋅\left( \lim_{x→a}\;(ten−a)\correct)+\lim_{x→a}f(a)\\[4pt]
&=f'(a)⋅0+f(a)\\[4pt]
&=f(a). \end{align*}\)

Therefore, since \(f(a)\) is defined and \(\displaystyle \lim_{x→a}f(x)=f(a)\), we conclude that \(f\) is continuous at \(a\).

□

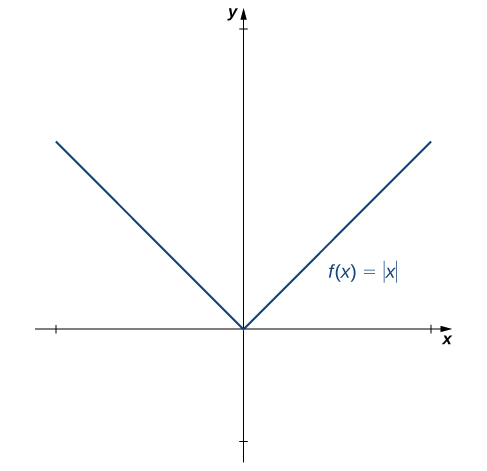
Nosotros accept but proven that differentiability implies continuity, only now we consider whether continuity implies differentiability. To decide an reply to this question, we examine the role \(f(x)=|x|\). This function is continuous everywhere; notwithstanding, \(f'(0)\) is undefined. This observation leads us to believe that continuity does not imply differentiability. Let'due south explore further. For \(f(x)=|10|\),

\(f'(0)=\displaystyle \lim_{x→0}\frac{f(10)−f(0)}{x−0}= \lim_{x→0}\frac{|10|−|0|}{x−0}= \lim_{ten→0}\frac{|x|}{10}\).

This limit does not exist considering

\(\displaystyle \lim_{10→0^−}\frac{|x|}{10}=−1\) and \(\displaystyle \lim_{x→0^+}\frac{|10|}{x}=1\).

Run across Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\): The function \(f(10)=|10|\) is continuous at \(0\) only is non differentiable at \(0\).

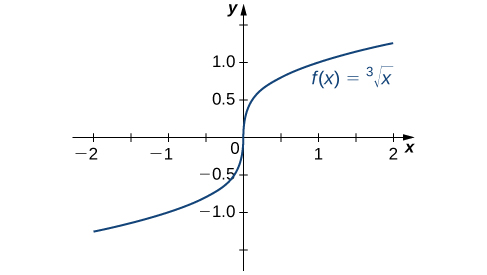
Let'south consider some additional situations in which a continuous office fails to be differentiable. Consider the function \(f(x)=\sqrt[3]{x}\):

\(f'(0)=\displaystyle \lim_{ten→0}\frac{\sqrt[3]{10}−0}{x−0}=\displaystyle \lim_{x→0}\frac{1}{\sqrt[three]{10^2}}=+∞\).

Thus \(f'(0)\) does not be. A quick wait at the graph of \(f(ten)=\sqrt[3]{x}\) clarifies the state of affairs. The function has a vertical tangent line at \(0\) (Figure \(\PageIndex{5}\)).

Effigy \(\PageIndex{5}\): The function \(f(10)=\sqrt[3]{x}\) has a vertical tangent at \(ten=0\). It is continuous at \(0\) but is not differentiable at \(0\).

The role \(f(x)=\begin{cases} x\sin\left(\frac{1}{x}\correct), & & \text{ if } 10≠0\\0, & & \text{ if } x=0\terminate{cases}\) also has a derivative that exhibits interesting behavior at \(0\).

We encounter that

\(f'(0)=\displaystyle \lim_{x→0}\frac{x\sin\left(1/ten\correct)−0}{x−0}= \lim_{x→0}\sin\left(\frac{i}{x}\correct)\).

This limit does not be, substantially considering the slopes of the secant lines continuously change direction equally they approach zero (Figure \(\PageIndex{6}\)).

Figure \(\PageIndex{half dozen}\): The part \(f(10)=\begin{cases} x\sin\left(\frac{i}{x}\right), & & \text{ if } 10≠0\\0, & & \text{ if } x=0\end{cases}\) is not differentiable at \(0\).

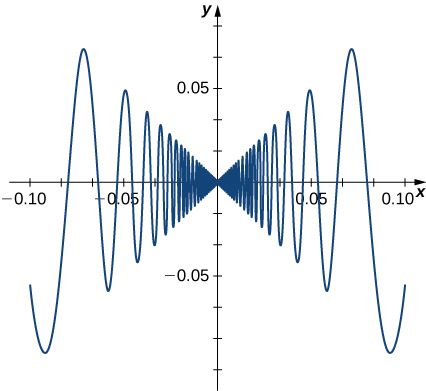
In summary:

1. We find that if a part is non continuous, it cannot be differentiable, since every differentiable function must be continuous. However, if a part is continuous, it may nonetheless fail to be differentiable.
2. We saw that \(f(ten)=|x|\) failed to exist differentiable at \(0\) because the limit of the slopes of the tangent lines on the left and right were not the same. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) From this nosotros conclude that in order to be differentiable at a point, a function must be "smooth" at that signal.
3. Every bit nosotros saw in the case of \(f(x)=\sqrt[3]{x}\), a function fails to be differentiable at a indicate where there is a vertical tangent line.
4. As we saw with \(f(x)=\brainstorm{cases}ten\sin\left(\frac{1}{x}\correct), & & \text{ if } x≠0\\0, & &\text{ if } 10=0\end{cases}\) a function may fail to exist differentiable at a point in more complicated ways as well.

Instance \(\PageIndex{4}\): A Piecewise Function that is Continuous and Differentiable

A toy company wants to design a track for a toy car that starts out forth a parabolic bend and then converts to a direct line (Figure \(\PageIndex{7}\)). The part that describes the track is to have the form \(f(x)=\brainstorm{cases}\frac{1}{10}x^2+bx+c, & & \text{ if }x<−10\\−\frac{i}{4}x+\frac{5}{2}, & & \text{ if } 10≥−x\end{cases}\) where \(ten\) and \(f(ten)\) are in inches. For the motorcar to move smoothly along the rails, the office \(f(x)\) must exist both continuous and differentiable at \(−x\). Find values of \(b\) and \(c\) that make \(f(10)\) both continuous and differentiable.

Figure \(\PageIndex{7}\): For the machine to motility smoothly along the track, the function must be both continuous and differentiable.

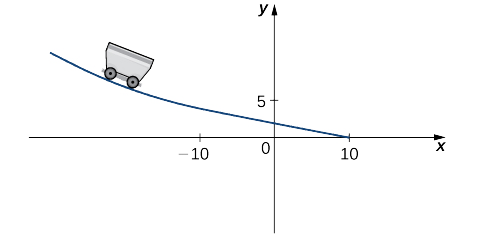
Solution

For the office to be continuous at \(ten=−10\), \(\displaystyle \lim_{x→10^−}f(x)=f(−x)\). Thus, since

\(\displaystyle \lim_{x→−10^−}f(ten)=\frac{1}{x}(−10)^ii−10b+c=x−10b+c\)

and \(f(−10)=5\), we must have \(ten−10b+c=v\). Equivalently, we accept \(c=10b−five\).

For the function to be differentiable at \(−10\),

\(f'(10)=\displaystyle \lim_{ten→−x}\frac{f(ten)−f(−10)}{x+10}\)

must exist. Since \(f(x)\) is defined using different rules on the right and the left, nosotros must evaluate this limit from the right and the left then set them equal to each other:

\(\displaystyle \brainstorm{align*} \lim_{10→−10^−}\frac{f(ten)−f(−10)}{x+10} &= \lim_{ten→−x^−}\frac{\frac{1}{10}ten^2+bx+c−v}{x+10}\\[4pt]
&= \lim_{x→−10^−}\frac{\frac{1}{10}x^2+bx+(10b−v)−5}{ten+10} & & \text{Substitute }c=10b−5.\\[4pt]
&= \lim_{x→−10^−}\frac{10^2−100+10bx+100b}{10(x+10)}\\[4pt]
&= \lim_{x→−10^−}\frac{(10+10)(x−ten+10b)}{10(x+10)} & & \text{Cistron by grouping}\\[4pt]
&=b−2 \end{align*}\).

We likewise have

\(\displaystyle \brainstorm{align*} \lim_{ten→−10^+}\frac{f(x)−f(−10)}{10+ten} &= \lim_{x→−ten^+}\frac{−\frac{1}{iv}10+\frac{5}{2}−5}{ten+10}\\[4pt]
&= \lim_{x→−ten^+}\frac{−(x+10)}{iv(x+10)}\\[4pt]
&=−\frac{1}{4} \end{align*}\).

This gives us \(b−two=−\frac{1}{4}\). Thus \(b=\frac{7}{four}\) and \(c=10(\frac{7}{4})−5=\frac{25}{ii}\).

Do \(\PageIndex{3}\)

Find values of a and b that make \(f(x)=\begin{cases}ax+b, & & \text{ if } x<3\\x^2, & & \text{ if } 10≥3\end{cases}\) both continuous and differentiable at \(three\).

Hint

Apply Example \(\PageIndex{iv}\) as a guide.

Reply

\(a=6\) and \(b=−ix\)

Higher-Lodge Derivatives

The derivative of a part is itself a office, so we tin can find the derivative of a derivative. For case, the derivative of a position function is the rate of alter of position, or velocity. The derivative of velocity is the rate of modify of velocity, which is dispatch. The new function obtained past differentiating the derivative is called the second derivative. Furthermore, we can continue to take derivatives to obtain the third derivative, fourth derivative, and then on. Collectively, these are referred to equally college-order derivatives. The note for the higher-club derivatives of \(y=f(x)\) can be expressed in any of the following forms:

\(f''(10),\; f'''(x),\; f^{(4)}(x),\; …\; ,\; f^{(due north)}(x)\)

\(y''(x),\; y'''(x),\; y^{(4)}(x),\; …\; ,\; y^{(n)}(x)\)

\(\dfrac{d^2y}{dx^ii},\;\dfrac{d^3y}{dy^three},\;\dfrac{d^4y}{dy^four},\;…\;,\;\dfrac{d^ny}{dy^north}.\)

Information technology is interesting to note that the notation for \(\dfrac{d^2y}{dx^ii}\) may be viewed as an attempt to express \(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\correct)\) more compactly.

Analogously, \(\dfrac{d}{dx}\left(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\right)=\dfrac{d}{dx}\left(\dfrac{d^2y}{dx^2}\right)=\dfrac{d^3y}{dx^3}\).

Example \(\PageIndex{5}\): Finding a 2d Derivative

For \(f(x)=2x^ii−3x+i\), detect \(f''(10)\).

Solution

First find \(f'(x)\).

Substitute \(f(x)=2x^2−3x+one\) and \(f(x+h)=two(x+h)^2−3(x+h)+1\) into \(f'(x)=\displaystyle \lim_{h→0}\dfrac{f(x+h)−f(ten)}{h}.\)

\(f'(x)=\displaystyle \lim_{h→0}\frac{(2(x+h)^2−3(ten+h)+ane)−(2x^two−3x+1)}{h}\)
\(=\displaystyle \lim_{h→0}\frac{4xh+h^ii−3h}{h}\)	Simplify the numerator.
\(=\displaystyle \lim_{h→0}(4x+h−three)\)	Factor out the \(h\) in the numerator and cancel with the \(h\) in the denominator.
\(=4x−3\)	Take the limit.

Next, detect \(f''(ten)\) past taking the derivative of \(f'(x)=4x−iii.\)

\(f''(x)=\displaystyle \lim_{h→0}\frac{f'(x+h)−f'(10)}{h}\)	Use \(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\) with \(f ′(x)\) in place of \(f(x).\)
\(=\displaystyle \lim_{h→0}\frac{(four(x+h)−3)−(4x−three)}{h}\)	Substitute \(f'(x+h)=4(ten+h)−iii\) and \(f'(x)=4x−3.\)
\(=\displaystyle \lim_{h→0}4\)	Simplify.
\(=four\)	Take the limit.

Exercise \(\PageIndex{4}\)

Discover \(f''(10)\) for \(f(x)=ten^2\).

Hint

We found \(f'(x)=2x\) in a previous checkpoint. Apply Equation \ref{derdef} to observe the derivative of \(f'(ten)\)

Answer

\(f''(x)=2\)

Example \(\PageIndex{vi}\): Finding Acceleration

The position of a particle forth a coordinate centrality at time \(t\) (in seconds) is given by \(s(t)=3t^2−4t+one\) (in meters). Find the function that describes its dispatch at time \(t\).

Solution

Since \(v(t)=s′(t)\) and \(a(t)=5′(t)=s''(t)\), we begin past finding the derivative of \(southward(t)\):

\(\displaystyle \begin{align*} southward′(t) &= \lim_{h→0}\frac{s(t+h)−s(t)}{h}\\[4pt]
&=\lim_{h→0}\frac{iii(t+h)^2−4(t+h)+1−(3t^2−4t+1)}{h}\\[4pt]
&=6t−4. \end{align*}\)

Adjacent,

\(\displaystyle \brainstorm{align*} s''(t)&= \lim_{h→0}\frac{southward′(t+h)−s′(t)}{h}\\[4pt]
&=\lim_{h→0}\frac{6(t+h)−4−(6t−4)}{h}\\[4pt]
&=6. \end{align*}\)

Thus, \(a=6 \;\text{chiliad/s}^2\).

Practise \(\PageIndex{5}\)

For \(southward(t)=t^3\), find \(a(t).\)

Hint

Employ Instance \(\PageIndex{vi}\) as a guide.

Answer

\(a(t)=6t\)

Cardinal Concepts

• The derivative of a role \(f(x)\) is the function whose value at \(x\) is \(f'(x)\).
• The graph of a derivative of a role \(f(ten)\) is related to the graph of \(f(x)\). Where \(f(ten)\) has a tangent line with positive gradient, \(f'(ten)>0\). Where \(f(10)\) has a tangent line with negative slope, \(f'(x)<0\). Where \(f(x)\) has a horizontal tangent line, \(f'(x)=0.\)
• If a part is differentiable at a betoken, then it is continuous at that betoken. A function is not differentiable at a point if it is non continuous at the signal, if it has a vertical tangent line at the betoken, or if the graph has a precipitous corner or cusp.
• College-order derivatives are derivatives of derivatives, from the second derivative to the \(n^{\text{thursday}}\) derivative.

Primal Equations

• The derivative part

\(f'(x)=\displaystyle \lim_{h→0}\frac{f(10+h)−f(10)}{h}\)

Glossary

derivative role

gives the derivative of a part at each signal in the domain of the original function for which the derivative is defined

differentiable at \(a\)

a function for which \(f'(a)\) exists is differentiable at \(a\)

differentiable on \(S\)

a part for which \(f'(10)\) exists for each \(x\) in the open set \(S\) is differentiable on \(S\)

differentiable function

a function for which \(f'(10)\) exists is a differentiable function

higher-order derivative

a derivative of a derivative, from the 2d derivative to the \(n^{\text{th}}\) derivative, is called a higher-order derivative

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin "Jed" Herman (Harvey Mudd) with many contributing authors. This content past OpenStax is licensed with a CC-By-SA-NC 4.0 license. Download for free at http://cnx.org.

• Paul Seeburger (Monroe Customs Higher) added caption of the alternative definition of the derivative used in the proof of that differentiability implies continuity.

Source: https://math.libretexts.org/Bookshelves/Calculus/Book%3A_Calculus_(OpenStax)/03%3A_Derivatives/3.2%3A_The_Derivative_as_a_Function

Posted by: gravescolmilluke.blogspot.com

Share this post